코코와 나
Deep Q network (DQN) 본문
이전 게시글에서 강화 학습을 위한 Discount rate($\gamma$)와 가치 함수(value function)에 대해서 정리 했었습니다.
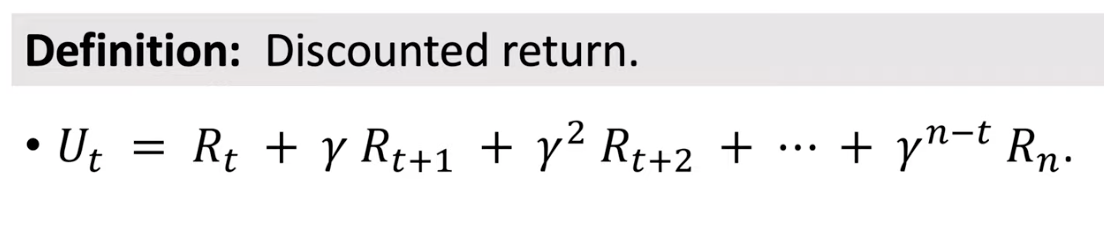
$\gamma$는 미래의 보상에 대한 잠정적인 할인율을 episode length에 비례해 곱해주는 값이였습니다.
value function은 상태의 value에 대한 수치적 표상 입니다.

이를 통해 Agent는 최상의 value를 갖는 위치를 찾아 움직이는 형태로 동작하며 최적의 경로를 searching 합니다.
해결하고자 하는 문제가 제약적이고 비좁은 경우에는 Agent와 ㄷEnv에 대한 정보 또한 narrow하기 때문에 value function에 대한 충분한 계산으로 최적의 경로를 searching 할 수 있었습니다.
하지만 이를 확장하는데는 몇 가지 문제가 수반됩니다.
그 중 가장 큰 문제는 다음과 같습니다.
Env의 크기가 관측하지 못하거나 관측 가능하더라고 충분히 큰 경우 :
이와 같은 경우에는 가치 함수나 Q-learning을 위한 Q-value table 자체도 비례적으로 커져야 합니다. 예를 들어 3차원 환경에서 각 차원의 크기가 2배로 커기는 경우에는 $2^3=8$ 즉 8배 만큼의 가치함수의 크기 증가를 메모리로서 관리해야 합니다. 이 경우에는 다수번의 step을 통해서 가치 함수 계산을 갱신해야 하므로 연산 비용 및 메모리 비용이 비례적으로 상승합니다.
이를 해결하기 위해서는 Env의 크기에 영향을 받지 않으면서도 효과적으로 가치 함수를 연산하고 추론할 수 있는 방법론이 요구됩니다.
Q-function
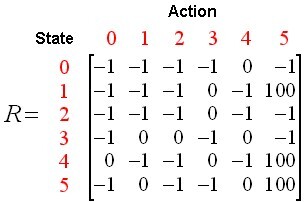
가치 함수는 모든 상태공간을 잠재적인 가치로 치환했고 그중에서 가장 높은 가치를 갖는 위치로 반복적으로 이동하며 최적의 해를 찾아왔습니다.

그에 반해 Q-function은 상태를 행동으로 치환하는 함수 입니다. Q-function은 각 상태에서 가장 높은 Q 값을 갖는 행동을 선택해서 움직입니다. 이때의 Q-function을 정책함수라고도 합니다.
여기서 Q값을 업데이트 하기 위해서는 현재와 미래에 대한 가치를 동시에 고려할 필요가 있습니다.
다시 말해 현재 가치 $Q(s,a)$를 통해 도출되는 다음 상태 $Q(s^',a^')$를 동시에 고려하는 셈입니다.
따라서 함수의 실제 가치는 현재의 선택과 이를 통해 불러오는 미래결과의 합 입니다.
우리는 위에서 discount factor($\gamma$)에 대해서 이야기를 했습니다. 지금의 가치는 미래의 가치보다 상대적으로 중요하기 때문에 감가율을 적용하게 되면 수식은 다음과 같이 수정됩니다.
$Q(s,a) = R + \gamma Q(s',a')$
그리고 우리는 Q값이 상태에 대한 최선의 action을 선택하는 과정의 일부라고 했으므로 다음과 같이 바꿀수 있겠습니다 .
$Q(s,a) = R + \gamma max(Q(s',a'))$
이를 최적화 하는 것이 최종적인 목표 입니다.
우리가 일반적으로 어떠한 수치를 가늠하기 위해서는 다수번을 시행하고 그 결과를 대충 평균을 내어봅니다.
다시 말해
$Value = \sum_{n=1}^{x}v_n$
입니다. 그리고 코드를 짤때 업데이트 될때마다 새로운 값을 다시 더하고 나누는 것은 연산의 비효율을 초래하기 때문에 평균은 다음과 같이 수정됩니다.
$UpdateValue = \frac{1}{n}(\sum_{x=1}^{n-1}v_i + v_n)$
$ = \frac{1}{n}((n-1)\times\frac{1}{n-1}\sum_{x=1}^{n-1}v_x+v_n)$
$ = value + \frac{1}{n}(v_n-value)$
평균을 구하는 식이 기존의 평균과 새로운 입력의 차이에 대한 비율의 합으로 변경되었습니다.
이 식을 이용하면 Q값을 추론하는데 다음과 같이 수행할 수 있게 됩니다.
$Q(s,a) = Q(s,a) + \alpha(R+\gamma max(Q(s',a'))-Q(s,a))$
하지만 이렇게 구해진 Q값들중 가장 높은 수치만 골라서 움직인다면 과연 최적의 결과를 도출 할 수 있을까요??

이와 같이 눈앞의 혹은 근 시안적인 결과에 만족하고 Agent가 반복된 행동을 수행하는것을 막기 위해 엡실론-그리디 방식을 통해 다양한 루트를 탐색하고 잠재적인 다른 보상을 찾을 수 있도록 유도합니다.
예를들어 $\epsilon$이 0.1이라면 90% 확률로 최적의 행동을 수행하고 잔여 10%확률로 무작위행동을 수행해 또다른 보상을 탐색하게 합니다.
DQN

이제 다시 이야기를 할 수 있게 되었습니다.

상태공간이 커지게 되면 state-action table의 규모가 커지게 되고 연산의 횟수로 늘어나게 됩니다.
이를 방지하고 보다 복잡한 문제를 해결하고 비선형 함수를 근사하기 위해 Q테이블 대신에 network를 삽입합니다.
'기계학습' 카테고리의 다른 글
| Temporal Diff & SARSA (0) | 2022.12.25 |
|---|---|
| Monte Carlo Method(몬테카를로 방법) (0) | 2022.12.25 |
| POMDP(partially observable Markov decision process) (1) | 2022.12.22 |
| Markov Decision Process (0) | 2022.12.22 |
| 9. SVM (Support Vector Machine) (0) | 2021.08.31 |