DQN(Deep Q-network)

Markov Decision process

다시 한번 MDP에 대해서 정리 하고 갑니다.

1. Agent: 

   강화 학습 에이전트는 올바른 결정을 내리기 위해 훈련하는 엔터티입니다. 최적의 결정을 위해 다양한 형태를 가질 수 있음을 유념합니다.

2. Environment:

   환경은 에이전트가 상호 작용하는 주변 환경(설정, 제약 등)입니다. 이러한 설정에서 에이전트는 환경을 조작할 수 없습니다. 다만 아래의 Action, 행동을 통해서만 환경과 상호작용 합니다. 

3. State:

   상태는 에이전트의 현재 상황을 정의합니다. 이는 이전 결정 , action ,보상 등에 의해 다양해 질 수 있습니다.

4. Action:

   에이전트가 현재 episode에서의 선택을 의미합니다. 에이전트가 수행할 수 있는 일련의 작업(결정)을 미리 알고 제한 할 수 있습니다. 예상되지 않는 결정은 내리지 않으며 예상되는 결정 안에서 최적의 결정만을 수행합니다.

5. Policy:

   정책은 행동을 선택하는 과정입니다. 실제로는 일련의 작업에 할당된 확률 분포입니다. 확률 분포라 함은 선택이 확률적으로 일어날 수 있다는 말 입니다. 유의미한 혹은 빈번한 행동은 높은 확률을 가지며 그 반대도 마찬가지입니다. 행동의 확률이 낮다고 해서 전혀 선택되지 않는다는 의미는 아닙니다.

---

Markov Property

에이전트는 어떤 상황에 놓여져 있습니다. 그리고 해당 상황에서 어떤 선택을 통해 다음 상황으로 변화 할 수 있습니다.

여기서 에이전트가 놓여 있는 상황이 State 입니다.

이제 마르코프 속성에 따르면 에이전트의 현재 상태는 바로 이전에 놓여져 있던 상태에서 일부 변질된것에 불과 합니다. 좀 더 나아가 이전 상태는 아마 그 이전 상태의 어떤 행동의 결과일 것입니다.

즉 지금 상태는 이전 상태의 변질이지 이전전 (2단계 전) 상태에 의존하지 않습니다. 마찬가지로 다음 상태는 지금 상태의 변질입니다.

식에 의하면 상태 $S_t$가 마르코프가 되려면 다음 상태 $S_{t+1}$가 될 확률은 현재 상태에 의존해야 하며 나머지 과거와는 독립적이여야 합니다.

---

Markov Process Explained

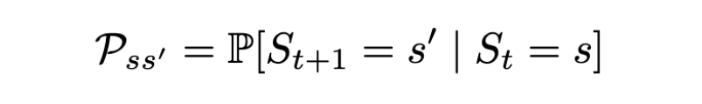
Markov 프로세스는 상태 가 (S, P) 가 어떠한지에 의해 정의되며 P 는 상태 전이 확률입니다. 모든 상태가 Markov 속성을 따르는 임의 상태의 시퀀스로 구성됩니다 .S S₁, S₂

만약 상태에서 어떤 행동을 통해 보상을 받을 수 있다면 그리고 그 보상을 최대화 한다고 생각해 봅니다.

그러면 이득이 되는 환경을 위해 보상을 설정 할 수 있습니다. 이 보상을 목적을 위해 fitting 되어야 합니다 .

이를 MRP(마르코프 보상 프로세스)라고 합니다.

---

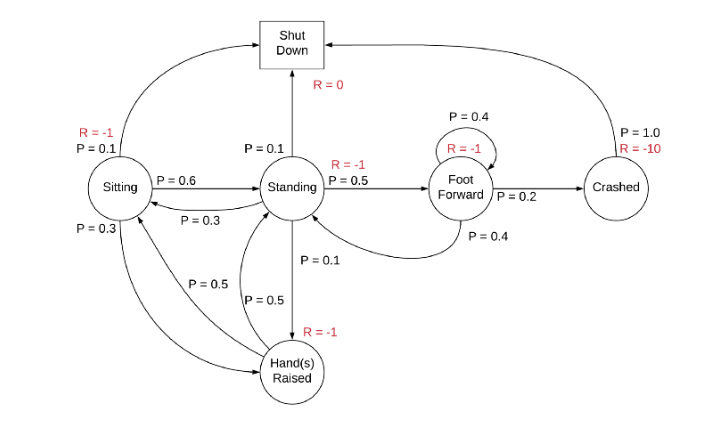
MDP(마르코프 결정 프로세스)

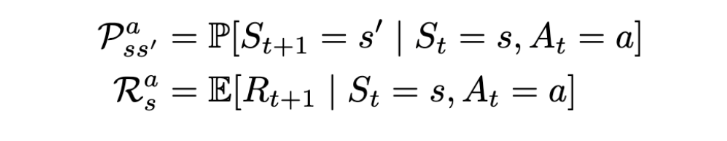
Markov 결정 프로세스(MDP)는  (S, A, P, R, γ)로 정의됩니다. 여기서 A 는 일련의 action 즉 행동입니다. 본질적으로 행동과 그에 따른 보상이 있는 MRP(마르코프 보상 체계)입니다.

여기서 행동은 Markov 프로세스에 대한 action 제어를 이끌어낼 수 있습니다. 

이전에는 상태 전이 확률과 상태 보상이 다소 확률적(확률 분포를 따르는 무작위)이었습니다.

그러나 MRP가 되면서 보상과 다음 상태도 에이전트가 선택한 작업에 따라 달라집니다. 기본적으로 에이전트는 이제 각 행동과 그 결과를 확률적이지만 어느 정도 제어하게 된 셈입니다.

---

Return (Final result)

보상은 하나의 선택에 의해 일시적 입니다. 에이전트의 최적의 선택의 연속이 장기적으로는 최적의 보상을 놓칠 수 있음을 고려해야 합니다. 위 식은 최종 리워드의 가중 합입니다.

이전 포스트에서도 말했듯이 지금의 보상은 미래의 보상보다 가치 있습니다. 그러므로 위처럼 가중되는 가치에 의해 현재와 미래 사이에서 보상을 조율할 수 있습니다.

---

$\gamma$(Discount Factor)

위 수식의 변수 γ ∈ [0, 1]는 미래 보상에 대한 일종의 할인입니다. 할인의 이면에 있는 본질은 미래 보상에 대한 확실성이 없다는 것입니다. 최대의 보상을 위해 미래 보상을 고려하는 것이 중요하지만 잠재적인 보상의 기여가 불확실 할 수 있으므로 (확률분포를 따르기 때문) 이를 제한하는 것도 마찬가지로 중요합니다.

---

Policy(π)

정책은 의사 결정(action) 뒤에 있는 결정논리를 정의합니다. RL 에이전트의 행동은 정책에 의 해 결정되는 셈 입니다.

다시 말해 s 를 전환하기 위한 actions a 의 확률 분포 입니다.

---

Value function

가치 함수는 현 상태에서 에이전트가 정책을 따르는 경우에 미래 보상에 대한 기댓값입니다.

기댓값이라는 단어에 유의합니다.

(𝑮𝑪𝒂𝒔𝒆 𝟏 * 𝑷𝑪𝒂𝒔𝒆 𝟏) + ... + (𝑮𝑪𝒂𝒔𝒆 𝑵 * 𝑷𝑪𝒂𝒔𝒆 𝑵)인 셈입니다.

즉 상태 가치 함수 v(s)는 state 에서 시작하는 기대되는 Return s입니다.

---

MARKOV 보상 프로세스(MRP)에 대한 BELLMAN 기대 방정식

벨만 방정식은 가치함수의 특성을 십분 활용합니다.

가치 함수를 두가지 요소로 쪼개 봅니다.

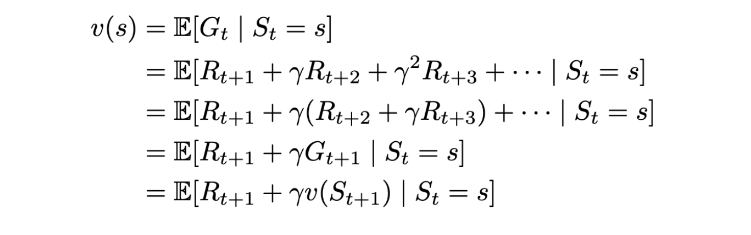
1. 즉각적인 보상 R_(t+1).

2. 미래 상태의 할인된 가치 γ x v(S_(t+1)).

왜 $E[R_{t+1}+\gamma G_{t+1}|S_t = s] = E[R_{t+1}+\gamma v(S_{t+1})|S_t = s]$일까요?

먼저 정의에 의해 (위 그림 참조)

$E[v(S_{t+1})|S_t = s] = E[E[G_{t+1}|S_{t+1}]|S_t = s]$입니다.

Law of iterated expectation에 의해 $E[E[X|Y]|Z] = E[X|Z]$ 입니다.

그러면 $E[E[G_{t+1}|S_{t+1}]|S_t = s] = E[G_{t+1}|S_t = s]$입니다.

이에

$E[G_{t+1}|S_t = s] = E[v(S_{t+1})|S_t = s]$입니다.

다시 처음으로 가서

$v(s) = E[R_{t+1}+\gamma G_{t+1} | S_t = s]$ 에서 $v(s) = E[R_{t+1} | S_t = s] + E[\gamma G_{t+1} | S_t = s]$로 기댓값은 쪼갤 수 있습니다.

그리고 계수는 꺼낼 수 있으므로

$v(s) = E[R_{t+1} | S_t = s] + \gamma E[G_{t+1} | S_t = s]$

$= E[R_{t+1} + \gamma v(S_t+1)|S_t = s]$이 됩니다.

Uploaded by N2T