우리는 지금까지 다양한 fixed된 환경에서의 강화 학습의 성능을 위한 replay memory와 target network 등을 알아본 바 있습니다.
본문 :
 https://arxiv.org/abs/1509.06461
https://arxiv.org/abs/1509.06461
하지만 어떤 확률적 환경에서 DQN과 Q-learning은 성능이 좋지 못한 경우가 있었습니다. 이는 어떤 작업이나 행동 (action)의 값을 과대 평가 → 과대한 Q값으로 인해 발생합니다. 다시말해 이러한 과대 평가는 Q-learning에서 를 예상 행동에 대한 근사치로 사용하는 경우에 양의 편향으로 인해 발생합니다.
본문 :
이를 회피하기 위한 Double Q-learning에서는 최대 를 과대로 추정하는 것을 방지하고 최저 값을 수용하는 형태로 동작합니다.

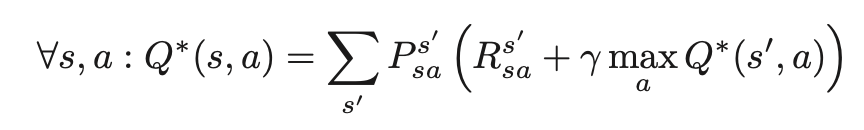
원래 Q-learning에서 $max$는 상태 $S’$에서 가장 값이 높은 $a$를 찾아 그 값에 $\gamma$를 곱해 미래 보상을 추정하고 이를 $Q(s,a)$와의 차이를 비용으로 Q-network를 훈련해 왔습니다.

하지만 여기서 action을 구성하고 Q값을 추정하는데 같은 네트워크를 사용하는데 있습니다. Q는 상한이 없는 신경망의 어떤 큰 값이 되고 그 값을 단순히 network의 출력으로 신뢰 하는것은 Q값이 점진적으로 증가 하는 형대로 동작하게 된다는 것을 의미 합니다. 즉 근사기 (신경망)은 optimal value에 대해 일정 값의 bias를 갖는다는 의미 입니다. 환경에 의한 노이즈 일 수 있습니다.

이에 저자가 최초에 제시한 방법은 2개의 Q-network를 사용하는 것입니다.

알고리즘에서 알 수 있듯이 값(action)을 추정하는 network와 Q값을 가져오는 네트워크를 따로 분리합니다.
$Q_A(s,a)=Q_A(s,a)+\alpha (R+\gamma Q_B(s′,argmaxQ_A(s′,a′))−Q_A(s,a))$
$Q_B(s,a)=Q_B(s,a)+\alpha (R+\gamma Q_A(s′,argmaxQ_B(s′,a′))−Q_B(s,a))$
두개의 식은 변수만 다를뿐 동일합니다. 다시 말해 A network에서 행동을 선택하고 B에서 Q값을 가져옵니다.
이렇게 두개의 Q-network를 같이 사용하는 것으로 과도한 Q 값을 막는다는데 있습니다.
하지만 이러한 두개의 네트워크는 이번이 처음이 아닙니다. 최초 DQN paper에도 target network가 있어 다수번의 업데이트를 한번씩 교체 해주는 것으로 모델의 발산을 막았습니다.
이에 위 논문에서는
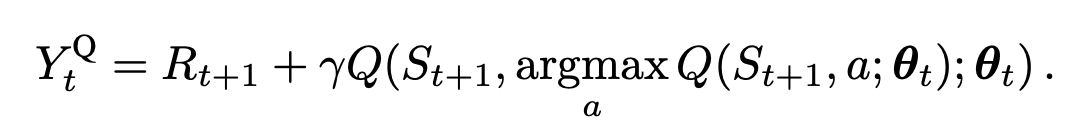
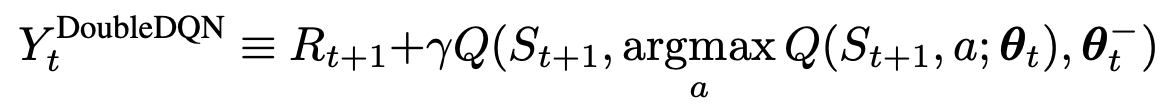
이처럼 action을 추정하는 network와 Q값을 가져오는 network를 분리 합니다.

그림을 보면 더 직관적으로 와닿습니다.
환경은 가장 높은 Q값을 action으로 받습니다. 이로 인한 변화된 강태를 상호작용하는 Q-network 가 있습니다. 그리고 DQN의 target network가 있습니다.
이는 임의의 N번의 update 이후에 한번씩 동기화 됩니다.
수식에서는 Q-network 가 A 이고 target network 가 B인 셈 입니다. 이때 가장 높은 Q 값을 target network에 대입 하는 형태 입니다. 그러면 다음 State에 대한 action은 target network가 추정하게 됩니다. 다시말해 현재 상태에 대한 action의 추정은 Q-network 가 , 다음 상태에 대한 추정은 target-network 가 하게 됩니다.
이를 통해 Q값의 발산을 막고 일부 제한된 환경에서 Agent의 훈련을 가속할 수 있습니다.
Uploaded by N2T