코코와 나
6. 고차원에서의 국소적 방법 본문
예측을 위한 기본적인 두가지 방법론을 뽑으라 하면 최소제곱 회귀와 k-최근접 이웃을 들수 있다.
이는 안정적이지만 편향된 모델과 덜 안정적이지만 분명히 덜 편향적인 k-최근접이웃 추정치 클래스가 해당된다.
적절하게 큰 훈련 데이터 집합이 있으면 k-최근접 이웃 평균법을 통해서 '언제나' 이론적으로 최적의 조건부 기댓값을 근사 할 수 있음을 우리는 알고 있다.
어떠한 x 든지 이에 가까운 관측치의 이웃을 찾을수 있고 평균 할 수 있기 때문이다.
하지만 이 접근법과 직관은 고차원에서는 쉽게 사상되지 않으며 이러한 현상을 차원의 저주라고 부른다.
차원의 저주에 대한 포스팅 또한 조만간 다루기로 한다.
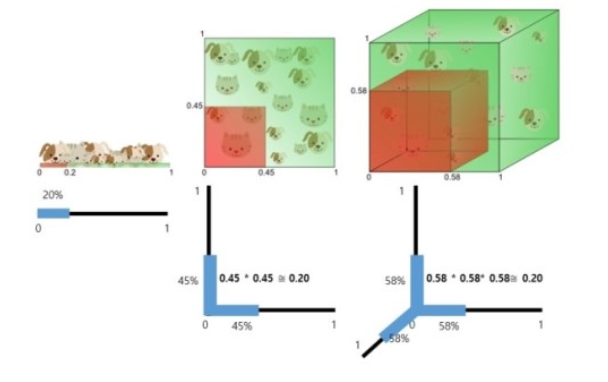
가정을 해 볼수 있다. P차원 유닛의 초입방체 내 균일하게 분포괸 입력값에 관한 최근접 이웃을 생각해 보자.
관측치의 부분 r 을 확보하기 위해 목표 지점에 관한 초 입방체로 된 이웃을 내보낸다고 생각하자.
이는 유닛 부피의 r 부분에 해당하게 되므로 모서리의 기대 길이는 e(r) = r^(1/p)가 될것이다.
10차원에서 입력의 전체 범위는 겨우 1에 불과 하다. 따라서 국소 평균을 구성하기 위해 데이터의 1%나 10%를 떼어내려면, 각 입력변수범위의 63%나 80%를 다루어야 한다는 말이다. 이러한 이웃은 더이상 '국소적'이라는 말이 어울리지 않는다.
r을 낮추는것 또한 크게 도움이 안되는데 적은 관측치를 평균 하면 적합의 분산이 커지기 때문이다.
따라서 많은 변수로 된 함수 복잡성은 차원과 함께 지수적으로 커질수 있으며 저차원에서의 함수와 같은 정확도로 이와 같은 함수를 추정하기 위해서는 훈련집합의 크기 또한 지수적으로 증가되어야 한다.
'기계학습' 카테고리의 다른 글
| 8. 규제가 있는 선형모델 (LASSO,ElasticNet) (0) | 2021.08.31 |
|---|---|
| 7. 규제가 있는 선형 모델(LIDGE) (0) | 2021.08.31 |
| 5. 확률 분포와 정보엔트로피 (0) | 2021.07.27 |
| 4. 시그모이드 함수 (0) | 2021.07.27 |
| 3. 이진 판단 문제 (0) | 2021.07.27 |