코코와 나
7. 규제가 있는 선형 모델(LIDGE) 본문
과대 적합을 감소 시키는 가장 좋은 방법은 규제를 가하는 것이다.
즉 모델을 제한하는 방법이다.
자유도를 주링면 데이터에 과대적합 되기 어려워 진다. 예를들어 다양호귀 모델을 규제하는 간단한 방법은 다항식의 차수를 감소 시키는 것이다.
선형회귀 에서는 보통 모델의 가중치를 제한 함으로서 규제를 가한다.
그중에서 릿지회귀에 대해서 알아보자
릿지 회귀는 규제가 단순 추가된 형태의 선형회귀 이다. 규제항 은 a*(sigma(x^2)) 이다.

여기서 하이퍼 파라미터 알파는 모델을 얼마나 많이 규제 할지 조절한다.
알파가 0 이면 릿지회귀는 선형 회귀와 같아진다.
알파가 아주 크면 모든 가중치가 0이 되어 결국 평균을 지나는 수평선이 된다.
이러한 릿지 회귀는 입력 특성의 스케일에 민감하기 때문에 수행하기 전에 데이터의 스케일을 맞추는 것이 중요하다.
이를 통해 모델의 분산을 줄지만 편향을 커지게 된다.
여기서 편향-분산 트레이드오프를 알아야 한다.
통계학과 머신러닝에서 나온 중요한 이론중의 하나는 모데르이 일반화 오차는 편향 + 분산 +줄일수 없는 오차로 구성된다.
편향
-일반화 오차 중에서 편향은 잘못된 가정으로 인한것이다. 예를 들어 데이터는 2차 인데 선형으로 간주한다던지 하는 경우를 말한다.
편향이 큰 모델은 훈련 데이터에 과소적합 된다.
분산
- 분산은 훈련 데이터에 있는 작은 변동에 모델이 과도하게 민감하게 반응하기 때문에 나타난다. 자유도가 높은 모델이 높은 분산을 가지기 쉬워 훈련 데이터에 과대적합 되는 경우가 있다.
줄일수 없는 오차
- 데이터 자체의 노이즈에 의한다. 이를 위해서는 노이즈를 감지해 제거하는 작업이 요구 된다.
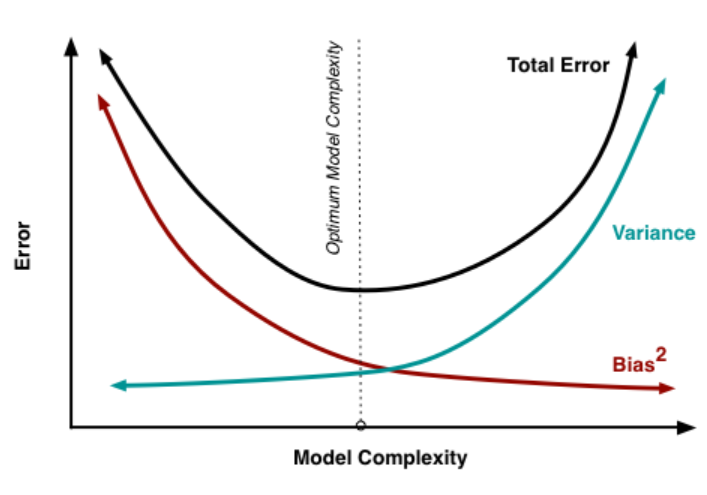
모델의 복잡도가 커지면 통산적으로 분산이 늘어나고 편향은 줄어든다. 반대로 모뎅이 단순해지면 편향이 커지고 분산이 작아진다.
이를 편향- 분산 트레이드 오프 라고 한다.
위에서 본것 처럼 분산이 줄고 편향이 커지게 된다는것은 릿지회귀를 통한 가중치의 규제는 모델을 단순화 시켜 과대 적합을 방지하는 효과를 불러온다.
'기계학습' 카테고리의 다른 글
| 9. SVM (Support Vector Machine) (0) | 2021.08.31 |
|---|---|
| 8. 규제가 있는 선형모델 (LASSO,ElasticNet) (0) | 2021.08.31 |
| 6. 고차원에서의 국소적 방법 (0) | 2021.08.31 |
| 5. 확률 분포와 정보엔트로피 (0) | 2021.07.27 |
| 4. 시그모이드 함수 (0) | 2021.07.27 |